适用于
分类(旧)
文本处理 剪贴板相关 脚本关键词
更多信息
| 分享时间 | 2025-03-04 20:52 |
| 最后更新 | 2025-04-04 20:45 |
| 修订版本 | 2 |
| 用户许可 | 可自己使用或修改,不可再分享 |
| Quicker版本 | 1.43.58 |
| 动作大小 | 11 KB |
简介
前期准备:必须已经下载pandoc,并添加到系统环境变量!!!
pandoc的GitHub项目网址:https://github.com/jgm/pandoc/releases/tag/3.6.3
使用步骤:选中LateX公式,然后使用动作自动转换后会打开一个临时的.docx文件,然后复制公式到需要的word文件中即可!注意及时关闭临时文件,否则影响下次转换!
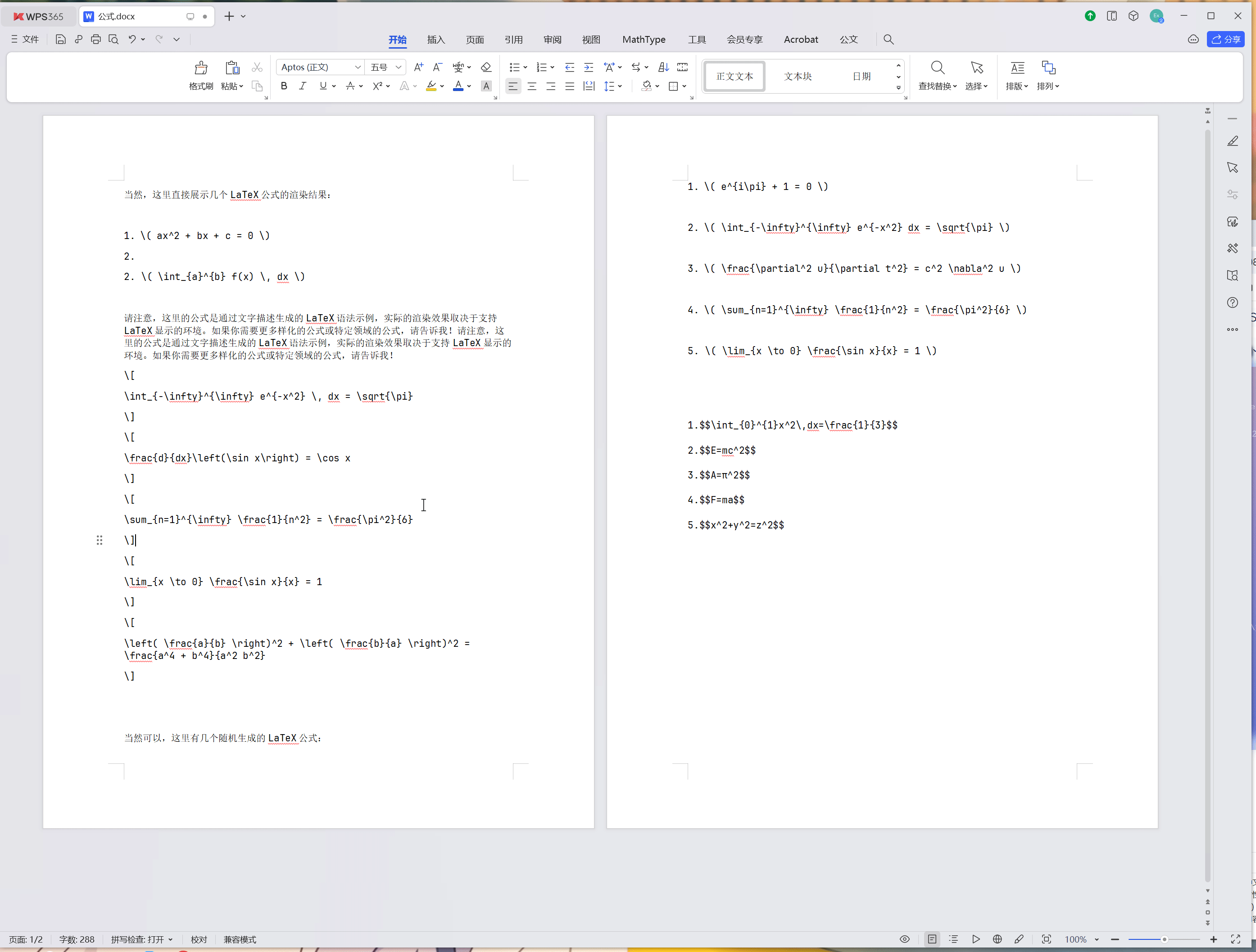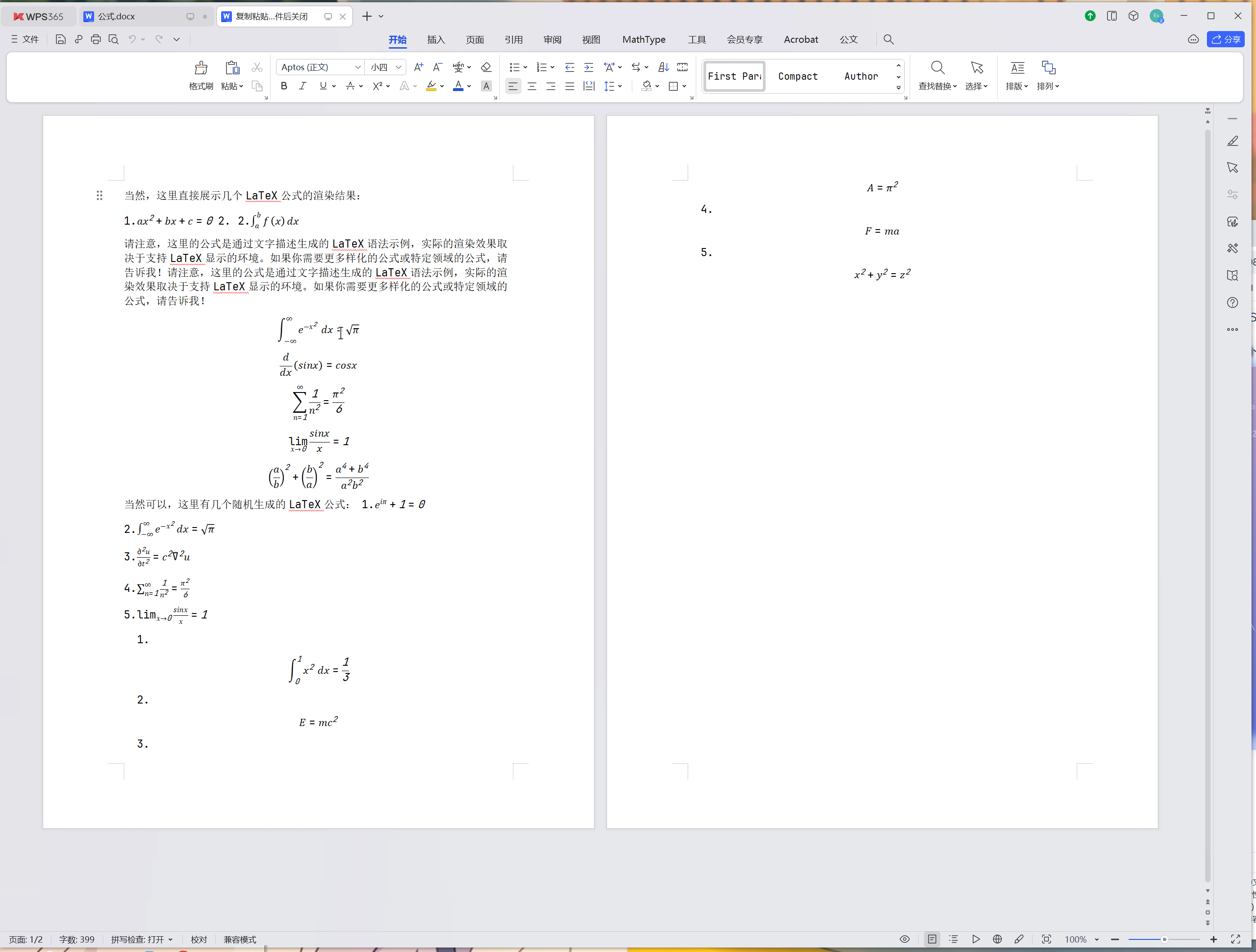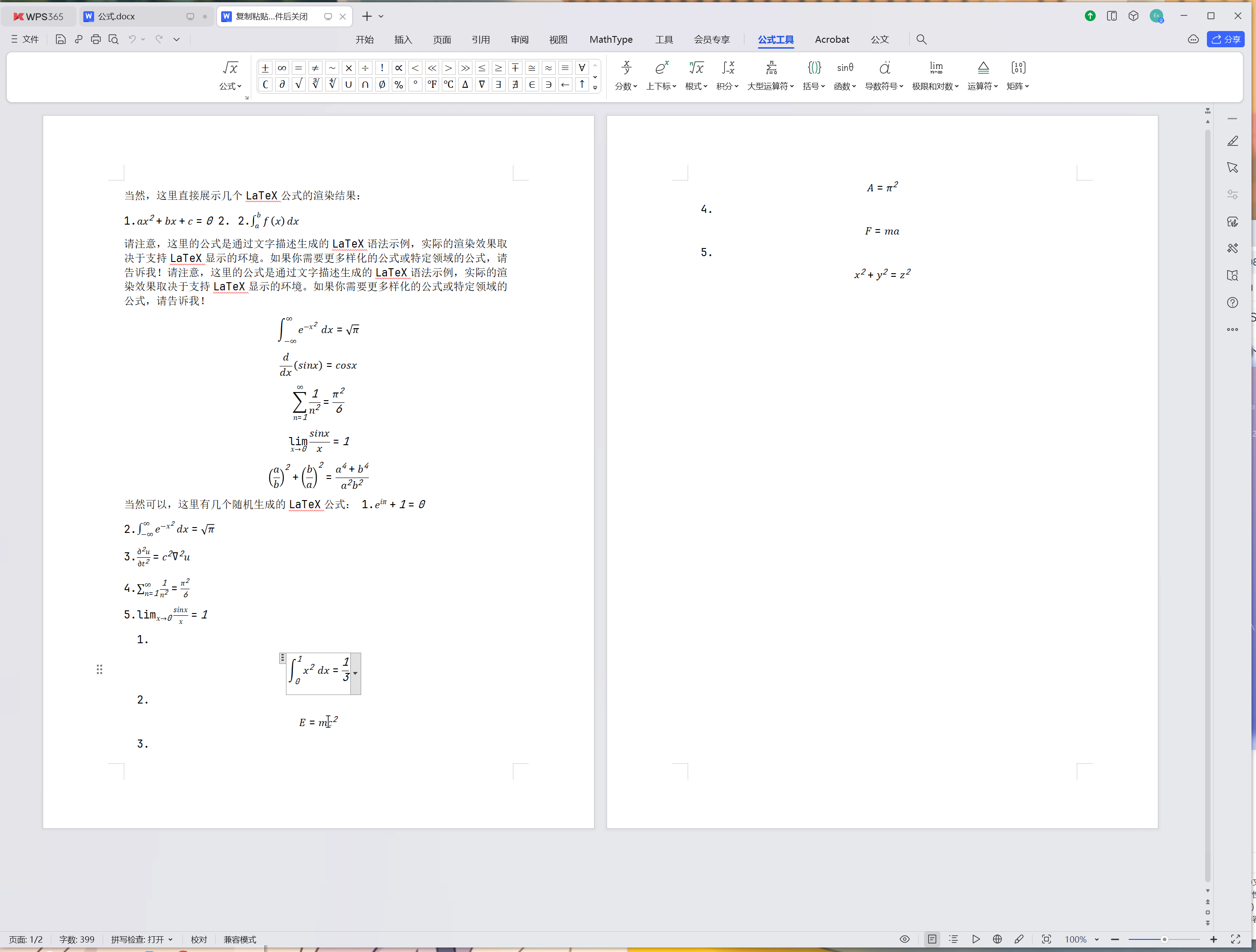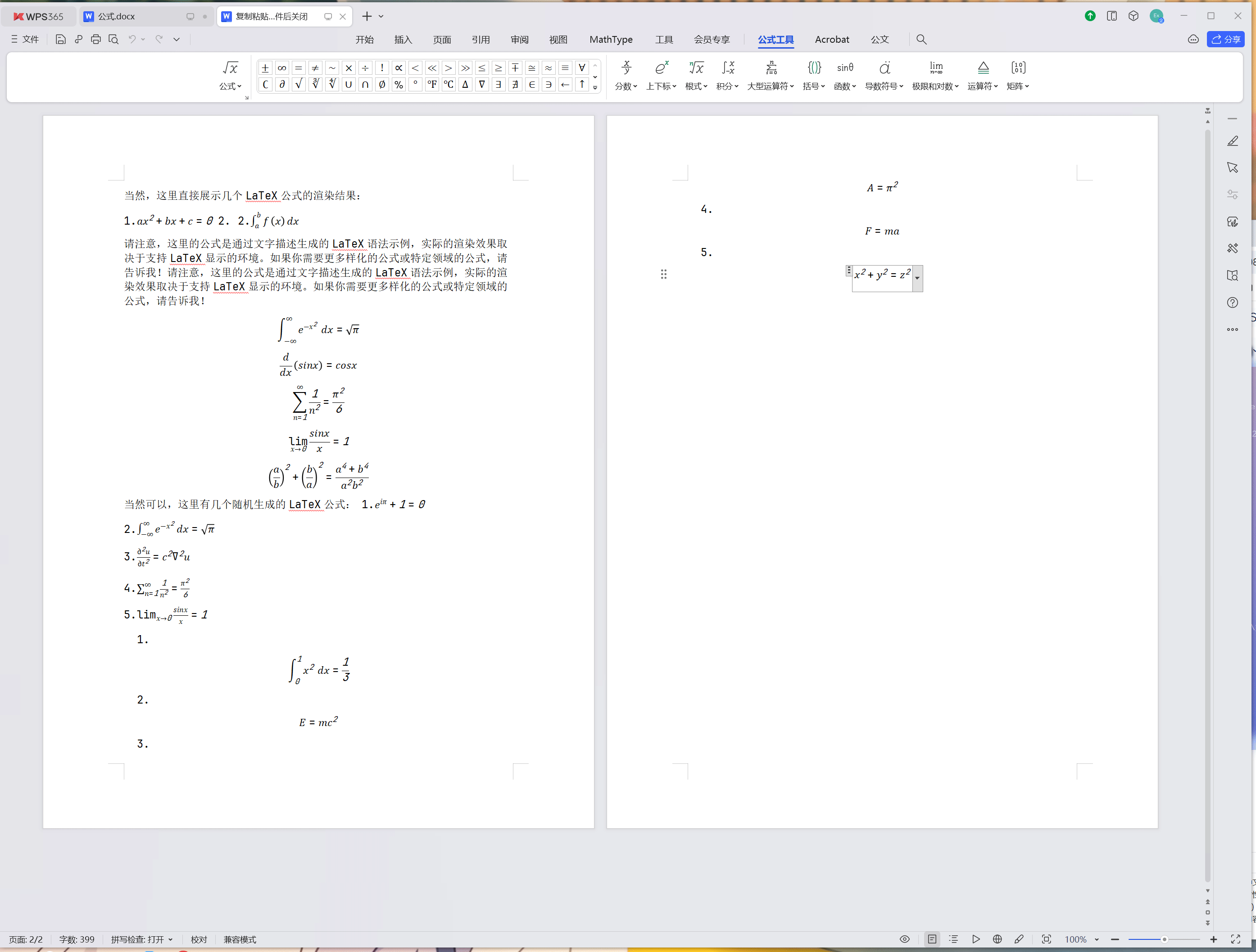
效果:读取剪切板LateX公式并转换为 WPS/MS Office 支持的可编辑公式格式
对于选中的LateX格式要求:要求 LateX公式 必须被如下任意的标识符包裹 $...$、$$...$$、\[...\]、\(...\) !!!否则容易出现公式部分转换混乱!
其他要求:选中文字尽量不要出现非文字符号,比如表情包、表情包版的数字序号、文字。(😃😄🤣😂🤩😙🤪😮💨0️⃣ 1️⃣ 2️⃣ 3️⃣ 4️⃣ 5️⃣ 6️⃣ 7️⃣ 8️⃣ 9️⃣🔠🔣🆗🆗🆘🈷🈶🈯🉐🈹🈲🈚🉑🈸🈴🈳㊗㊙🈺🈵)
常见问题1:如果某次选中的文字中公式过多肯会出现部分转换失败的情况,单独选中一个公式进行转换即可!
常见问题2:平常转换失败通常是公式中出现了多余的空行或空格,仔细检查一下再转换看看!
常见问题3:实在转换不成功的,可以去网页搜索 LateX编辑器 随便找一个在线网页进行转换,注意导出时选择导出为word文件即可!
不定期看评论,看到基本都会维护,不喜勿喷!!!
示例的复制LateX公式↓↓↓
当然,这里直接展示几个LaTeX公式的渲染结果:
1. \( ax^2 + bx + c = 0 \)
2.
2. \( \int_{a}^{b} f(x) \, dx \)
请注意,这里的公式是通过文字描述生成的LaTeX语法示例,实际的渲染效果取决于支持LaTeX显示的环境。如果你需要更多样化的公式或特定领域的公式,请告诉我!请注意,这里的公式是通过文字描述生成的LaTeX语法示例,实际的渲染效果取决于支持LaTeX显示的环境。如果你需要更多样化的公式或特定领域的公式,请告诉我!
\[
\int_{-\infty}^{\infty} e^{-x^2} \, dx = \sqrt{\pi}
\]
\[
\frac{d}{dx}\left(\sin x\right) = \cos x
\]
\[
\sum_{n=1}^{\infty} \frac{1}{n^2} = \frac{\pi^2}{6}
\]
\[
\lim_{x \to 0} \frac{\sin x}{x} = 1
\]
\[
\left( \frac{a}{b} \right)^2 + \left( \frac{b}{a} \right)^2 = \frac{a^4 + b^4}{a^2 b^2}
\]
当然可以,这里有几个随机生成的LaTeX公式:
1. \( e^{i\pi} + 1 = 0 \)
2. \( \int_{-\infty}^{\infty} e^{-x^2} dx = \sqrt{\pi} \)
3. \( \frac{\partial^2 u}{\partial t^2} = c^2 \nabla^2 u \)
4. \( \sum_{n=1}^{\infty} \frac{1}{n^2} = \frac{\pi^2}{6} \)
5. \( \lim_{x \to 0} \frac{\sin x}{x} = 1 \)
1.$$\int_{0}^{1}x^2\,dx=\frac{1}{3}$$
2.$$E=mc^2$$
3.$$A=π^2$$
4.$$F=ma$$
5.$$x^2+y^2=z^2$$
作者所声明的动作特征:
- 依赖第三方软件(如ffmpeg): pandoc
最近更新
| 修订版本 | 更新时间 | 更新说明 |
|---|---|---|
| 2 | 2025-04-04 20:45 |
看来两位朋友的评论,目前提到的问题都解决了
针对特殊的LateX命令进行了覆盖率95%+的针对性处理。目前基本上都能转换 更新一些动作介绍和常见问题解决办法 |
| 1 | 2025-03-05 13:22 |
1. 优化了使用体验,现在选中文本后就可以直接使用动作,不需要复制这个步骤了
2. 对AI生成的公式进行了针对性优化,现在AI生成的公式也可以直接转换了。(自动将 \[...\] 替换为 $$...$$、将 \(...\) 替换为 $...$) 3.对已知pandoc无法识别的内容进行了针对性替换,比如:\cos、\sin、\pi r 如有无法转换的公式可留言,看到会更新! |
| 0 | 2025-03-04 20:52 |


 京公网安备 11010502053266号
京公网安备 11010502053266号